Roman to Integer: Explaining problems and their solutions
Please Work!
When tackling a puzzle, especially a programming puzzle, there are many ways of approaching the problem. I know so many people who bask in pride at their one-liner that takes anyone, but them, 10 minutes to decipher. It can be especially problematic when you’re debugging on the manufacturing line and you see a scrolling, one-liner—a thing of beauty bringing you tears of fury.
I’ve decided to start looking for a job and I’m not sure yet what the title of my next chapter is. I feel like at the very least, more creative and deeper than, “if you’re stuck on a problem for 15 minutes, go ask someone.” That type of collaboration is valuable but I also love the moments when you sit with a problem and really get to understanding it. I’ve always been drawn to exploring why something works and what could work better. My exploration took me down 3D animation courses only to get vertigo while working in MAYA. It was super fun and I enjoyed it but I knew it was something I couldn’t do long term.
As I’ve been writing my blogs now, I’m finding a variety of topics I want to write about. Like for the past two days, I’ve been fantasizing about writing about how soap works. Why soap? Because I’m convinced most people don’t actually understand how it works and they just know it ‘cleans’ and that’s good enough.
So once again, maybe by interview habit, despite 5.5 years at Apple, I’ve found myself back working on LEET coding problems and after two years traveling, it’s slow going as expected. It always is because for whatever reason, it seems you’re always asked them despite it not having anything to do with your job function or how many years you’ve been out of college.
I on the other hand, love diving deep into why something works (and how it might work better)—like some crazy conspiracy theorist at a whiteboard. I used to go into long tangents about it until I noticed the glossy eyes. And now, the only time someone wants to hear all that is in an interview and I’ve fallen out of practice. Remember, interviewing is a skill. A skill of deconstructing your process well enough but not so much so that the other person loses interest… or can’t follow.
So, why not write about it?
The Problem: Roman to Integer
Ooooooo a problem, so exciting!
How many times a day do you think about the roman empire? Well now, we can easily read what your boyfriend has written across his chest… or if our impending tattoo is correct without Google’s AI-generated summary telling you something wrong. Ba-doomchee!
So, given a roman numeral, how do you convert it into an integer?
Roman numerals are represented by seven different symbols: I, V, X, L, C, D, M.
Each one is assigned a value:
I 1
V 5
X 10
L 50
C 100
D 500
M 1000
This progresses exactly how you would normally count with the number 3 written as III. The number 7 written as VII and the number 38 written as XXXVIII.
Roman numerals are normally written largest to smallest from left to right except for numbers that are one less than a multiple of 5, or are 4 mod 5, numbers congruent to -1 modulo 5.
For example: 4, 9, 14, 19…
By way of the romans, we subtract!
We denote subtraction by placing smaller value characters before the higher value ones but only with the following rules:
I (1) can be placed before V (5) and X (10) to make 4 and 9.
X (10) can be placed before L(50) and C (100) to make 40 and 90.
C (100) can be placed before D (500) and M (1000) to make 400 and 900.
With these rules, can we write a program that converts roman numerals into integers?
The Thinking Part:
Before I start programming or doing anything, I believe paper is our best friend. It helps grounds our thoughts. If I just start, even painting—incredibly fun and should be done—things just wind up a bit more messy. Sometimes, I really enjoy that. Other times when you’re looking at lines of code blurring together… it’s less so.
So, take some time to write down the problem and your initial thoughts.
That’s what I did.
I wrote the characters vertically with their value. Then I wrote some examples like:
27 —> XXVII 58 —> LVIII 1994—>MCMXCIV
I broke MCMXCIV into M (1000), CM (900), XC (90), IV (4)
But how do I go about telling the computer to look at 2 characters vs one?
Well, I can assign the character it’s value but wait! This jumble of letters is what’s called a string.
So we have to break the string apart into single characters.
And then once we do that, we can ask if the next character is a higher value than this character.
So, M is 1000.
Next character C is 100.
The next character is another M (1000).
Is C less than M?
Or C < M
Yes!
If it wasn’t, we’d just keep progressing.
Giving us a first clue!
If C < M:
Do a something.
Else:
Keep going.
Now we remember what the rules were. We have to subtract the character in front from the following character. ( IV —> V - I : 5 - 1 = 4 )
M - C
So, now we have:
If C < M:
M - C
Else:
Keep going
But then we have to ask, for how long? Giving us our next clue.
For (length of string):
If C < M:
M - C
Else:
Keep going
From there we can start asking ourselves questions. Like, how do we want to organize our characters and our values?
Do we want to assign values immediately like “V” = 5, “X” = 10 or {“V” : 5, “X”: 10}?
Or maybe we want to put them into two arrays?
We get into more personalized details like how do we want to convert a string into a list of characters? How do we turn those characters into an integer?
Programming
Now we start putting pieces together and start typing keeping our notes handy for more notes.
In Python, and several other languages, we start with a ‘class’ where all your ‘definitions’, or defining the program, will go.
We also know we are starting with a string (str) and returning an integer (int).
So we have:
class Solution:
def romanToInt(self, s: str) -> int:
Where ‘self’, is just the program saying “it’s me! Mario!” It’s the specific object this function belongs to.
’s’ in this case is the variable and here we have defined it as a string.
Then we are expecting a return value of an integer.
Next, I like to lay out the variables that we know just like how we defined them on our scrap paper.
Rom = ["I", "V", "X", "L", "C", "D", "M"]
Nu = [1, 5, 10, 50, 100, 500, 1000]
And let’s include information we know we might need. We might need another array once we turn our string into an array of characters. We might need another array once we turn those characters into numbers.
L1 = []
a = []
And we need a number returned. Let’s just say that starting value is 0.
num = 0
So now we have:
class Solution:
def romanToInt(self, s: str) -> int:
Rom = ["I", "V", "X", "L", "C", "D", "M"]
L2 = [1, 5, 10, 50, 100, 500, 1000]
L1 = []
a = []
num = 0 #int we’ll be returning
Now, we can do without some of these since we’re not sure what we’ll be using but at least we have them.
Next, we want to convert the characters to numbers.
We can think to ourselves, we have to create a list from our string, so:
L1 = list(str(s))
So now we realize we don’t need 2 new arrays. Go ahead and get rid of one of them.
But in Python, that step is redundant and we can just say:
for ch in s: # for every character in our string
x = (Rom.index(ch)) # Give us the index value of that character
y = Nu[x] # Now, give us the corresponding number
L1.append(y) # Now, let’s add our number to our new array!
Now, we have our original string represented in their corresponding values.
But we still don’t know what that number is and if we add them all up right now, we will likely come up with a greater value than the true value.
So now we go back to the formula on our scrap paper:
For (length of string):
If C < M:
M - C
Else:
Keep going
We have to remember, the computer reads every first value as 0, not 1.
So, we’re looking at the range of the length of our string, from 0 to the end.
If we only look at the length of our string, len(s), we get a number but Python only sees it as a number and cannot iterate over it. In other words, it needs a clear starting and ending point:
Like [0, 1].
But, if we have a string length of 5 and we take the range 0 to 5, we now have 6 iterations.
So, now we have to subtract an iteration.
Remembering we are using an array and not our string, we now have:
for i in range(len(L1) - 1): # for every value in range of the length of our array - 1 iteration
Now, we work inside our ‘for loop’.
If C < M:
M - C
Else:
Keep going
We need a value inside our array. To represent this, we use L1[i]. The next value would be L1[I+1]. Becoming:
if L1[i] < L1[I+1]:
Now, we need to subtract M - C.
We can write this as:
y = L1[i+1] - L1[i]
print(y)
Or we can just write the equivalent:
num -= L1[i]
Or num = num - L1[I] where we had earlier defined our returning value, num = 0
Now, if our number isn’t less than, we add that value to our number, num.
num += L1[i]
We should have:
for i in range(len(L1)-1):
if L1[i] < L1[i+1]:
y = L1[i+1] - L1[i]
print(y)
num -= L1[i]
else:
num += L1[i]
We can print out that number but we also have to remember range of length - 1 gives us:
0, 1, 2
Not 0, 1, 2, 3.
Since we’re always comparing the current character to the next one, we couldn’t safely check L1[i + 1]. We needed to loop over elements that had a “next one”
So, we simply add that last element to our number, num:
num += L1[-1]
return(num)
And there we have our solution!
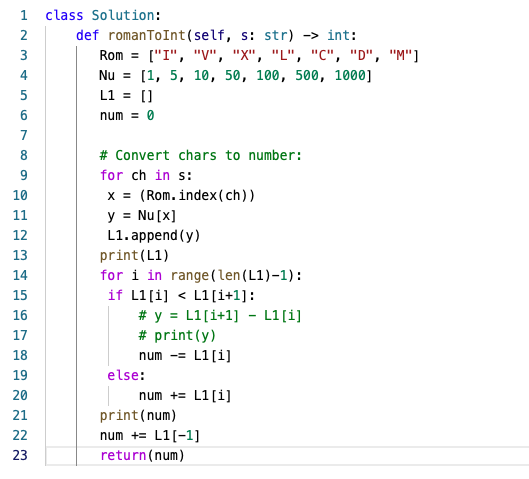
Solution:
class Solution:
def romanToInt(self, s: str) -> int:
Rom = ["I", "V", "X", "L", "C", "D", "M"]
Nu = [1, 5, 10, 50, 100, 500, 1000]
L1 = []
num = 0
# Convert chars to number:
for ch in s:
x = (Rom.index(ch))
y = Nu[x]
L1.append(y)
print(L1)
for i in range(len(L1)-1):
if L1[i] < L1[i+1]:
# y = L1[i+1] - L1[i]
# print(y)
num -= L1[i]
else:
num += L1[i]
print(num)
num += L1[-1]
return(num)
Now, there are much shorter ways of doing this.
For example this:
class Solution:
def romanToInt(self, s: str) -> int:
values = {
"I": 1, "V": 5, "X": 10, "L": 50,
"C": 100, "D": 500, "M": 1000
}
total = 0
for i in range(len(s) - 1):
if values[s[i]] < values[s[i + 1]]:
total -= values[s[i]]
else:
total += values[s[i]]
total += values[s[-1]]
return total
Or this:
class Solution:
def romanToInt(self, s):
val = {"I":1,"V":5,"X":10,"L":50,"C":100,"D":500,"M":1000}
total = 0
for i in range(len(s)-1):
total += -val[s[i]] if val[s[i]] < val[s[i+1]] else val[s[i]]
return total + val[s[-1]]
But I really enjoy the process and understanding how to get there. And if I’m having a shit day debugging, sometimes, the last thing I want to look at is several likes of:
total += -val[s[i]] if val[s[i]] < val[s[i+1]] else val[s[i]]
And that’s not even a scrollable one-liner.
So, if you made it this far, hahaha I hope you at least found this somewhat amusing.
Let me know in the comments if there’s something you’d like to learn about.